ei1333's page

点の進行方向

説明

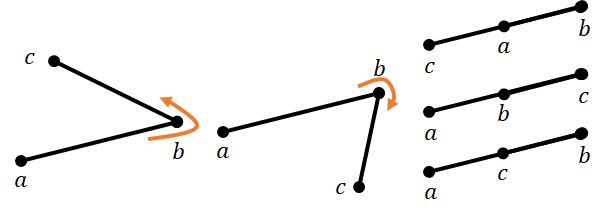
与えられた $3$ 点の位置関係は以下の $5$ つに分類できる。

• $a \to b$ 反時計回りの方向に $c$
• $a \to b$ 時計回りの方向に $c$
• $c \to a \to b$ の順に並ぶ
• $a \to b \to c$ の順に並ぶ
• $a \to c \to b$ の順に並ぶ

判定アルゴリズムは以下の通り。$a$ から $b$ へ向かうベクトルを $\vec b$, $a$ から $c$ へ向かうベクトルを $\vec c$ とする。

1. $\vec b \times \vec c \gt 0$ のとき, $\vec c$ は $\vec b$ から反時計回りの位置にあると判定できる。(外積は右ねじの方向を向く)
2. $\vec b \times \vec c \lt 0$ のとき, $\vec c$ は $\vec b $ から時計回りの位置にあると判定できる。
3. $\vec b \times \vec c = 0$ のとき $3$ 点が直線状に並ぶ。$\vec b \cdot \vec c \lt 0$ のとき, $c \to a \to b$ の順に並ぶと判定できる。($\cos \theta$ は $|\theta| \gt \frac \pi 2$ のとき負)
4. $|\vec b| \lt |\vec c|$ のとき, $a \to b \to c$ の順に並ぶと判定できる。
5. それ以外のとき, $a \to c \to b$ の順に並ぶと判定できる。

実装例

int ccw(const Point &a, Point b, Point c)
{
  b = b - a, c = c - a;
  if(cross(b, c) > EPS) return +1;
  if(cross(b, c) < -EPS) return -1;
  if(dot(b, c) < 0) return +2;
  if(b.norm() < c.norm()) return -2;
  return 0;
}