セグメント木(Segment-Tree)
説明
完全2分木である。区間に対する様々な演算が$O(\log N)$で実現できるが, ここでは一般的な操作であるRMQを実装している。
実装では木を配列で実現している。ノード $k$ について, 親ノードは $\frac {k - 1} {2}$, 子ノードは $2k+1, 2k+2$ である。
使い方
- $\mathrm{SegmentTree}(n)$: サイズ $n$ のセグ木の初期化
- $\mathrm{set}(k, x)$: $k$ 番目の要素に値 $x$ をセットする
- $\mathrm{build}()$: 構築する
- $\mathrm{rmq}(l, r)$: 区間 $[l, r)$ の最小値を求める
- $\mathrm{update}(k, x)$: $k$ 番目の要素を値 $x$ に変更する
計算量
- build: $O(N)$
- rmq, update: $O(\log N)$
実装例
応用 1: 区間加算
Starry-Sky-Tree と呼ばれる有名なセグメント木がある。このセグメント木では以下の $2$ つのクエリをサポートする。
- 区間 $[a, b)$ に一様に値 $x$ を加算する
- 区間 $[a, b)$ に最小値を求める
ここではその区間に一様に加算される値を持つ add 配列と, 区間の最小値を持つ small 配列を持つことによって実現している。
応用 2: 遅延評価
遅延評価というテクがある。遅延評価を使うと, 区間に対する演算操作の幅が大きく広がる。
応用 3: 2Dセグメント木
セグメント木のノードに平衡二分探索木をのせた 2Dセグメント木も可能(但し定数倍がかなり重い)。 以下の実装では長方形内の点の個数を求めるクエリと, 点の追加削除のクエリをサポートしている。
問題例
- 検証済AOJ DSL_2_A Range Minimum Query (RMQ)
- 検証済(応用3)CF #404 E. Anton and Permutation(Submittion: #25528699)
参考資料
BIT(Binary-Indexed-Tree)
説明
Fenwick Tree とも呼ばれる。数列に対し, ある要素に値を加える操作と, 区間和を求める操作をそれぞれ対数時間で行うことが出来るデータ構造。セグメント木や平衡二分探索木に比べ実装が非常に単純で, 定数倍も軽い。
使い方
- $\mathrm{sum}(k)$: 区間 $[0, k]$ の合計を求める(閉区間なので注意)
- $\mathrm{add}(k, x)$: 要素 $k$ に値 $x$ を加える
計算量
$O(\log N)$
実装例
応用: BIT上の二分探索
$\sum_{i=0}^{k} a_k \ge w$ となる最小の $k$ を求めたい(std::lower_bound() のイメージ)とき, BIT上を二分探索することで $O(\log N)$ 時間で行うことができる。
問題例
参考資料
素集合データ構造(Union-Find)
説明
集合を高速に扱うためのデータ構造。集合を合併する操作(unite), ある要素がどの集合に属しているか(find)を問い合わせる操作を行うことが出来る。
使い方
- $\mathrm{unite}(x, y)$: 集合 $x$ と $y$ を併合する. 併合済のとき $\mathrm{false}$, 未併合のとき $\mathrm{true}$ が返される
- $\mathrm{find(k)}$: 要素 $k$ が属する集合を求める
- $\mathrm{size(k)}$: 要素 $k$ が属する集合の要素の数を求める
計算量
$O(\alpha(n))$
$\alpha$ はアッカーマンの逆関数
実装例
応用 1: 2部グラフの頂点彩色
Union-Find を用いると $2$ 部グラフ判定とその副作用として彩色が可能。頂点を倍長して偶奇に分ける。隣接頂点を同じ色にするときは, $\mathrm{unite}(u, v)$ と $\mathrm{unite}(u+N, v+N)$, 異なる色にするときは $\mathrm{unite}(u+N, v)$ と $\mathrm{unite}(u, v+N)$ をする。
応用 2: データ構造をマージする一般的なテク
データ構造をマージする一般的なテク(Weighted-Union-Heuristic) は, Union-Find の unite 操作で常に大きい木の根が全体の根になるよう連結する(union-by-rank) の考え方と同様。
補足: 経路圧縮, ランクによる統合の計算量
経路圧縮, ランクによる統合の $2$ つの工夫をすると計算量は $1$ クエリあたり $O(\alpha(n))$ となるが, 経路圧縮あるいはランクによる統合片方だけ行うと $O(\log n)$ となる。[証明: アルゴリズムとデータ構造 p268-270]
問題例
- 検証済ATC 001_B Union Find
- AOJ DSL_1_A 互いに素な集合
- 検証済(応用1)CF #383 C. Arpa’s overnight party and Mehrdad’s silent entering(Submittion: #24955808)
- 検証済(応用1)CF #400 D. The Door Problem(Submittion: #24955583)
参考資料
平衡二分探索木(RBST)
説明
RBST(Randomized Binary Search Tree)は平衡二分探索木の一種。ランダムなノードを根にして期待値的に木の高さを$O(\log N)$ に抑える。
計算量
$O(\log N)$
実装例
問題例
ウェーブレット行列(Wavelet-Matrix)
説明
計算量
$O(\log N)$
実装例
合ってる可能性は1%くらいです...
問題例
トライ木(Trie)
説明
プレフィックス木とも呼ばれる。あるノードの配下の全てのノードには自身に対応する文字列に共通するプレフィックスがあり, ルートには空の文字列が対応している。
使い方
- $\mathrm{add}(str, id)$: 添字が $id$ の文字列 $str$ をTrieに追加する。
計算量
追加 $O(|m|)$
$m$: 追加する文字列
実装例
Aho-corasick に継承させたいので, そういう実装になってます。
応用: パトリシア木
特に, トライ木で子ノードが $1$ つしかないノードを子ノードとマージして縮約した木をパトリシア木(または基数木) と呼ぶ。無駄な探索を減らすことが出来る。
参考資料
スライド区間の昇順 k 個の和
説明
スライドする区間の昇順(降順) $k$ 個の総和を効率良く求めるデータ構造。
使い方
- $\mathrm{PrioritySumStructure}(k, order = \mathrm{INCREASE})$: 昇順(降順) $k$ 個に指定。
- $\mathrm{addElement}(k, x)$: $k$ 番目の要素 $x$ を追加する。
- $\mathrm{deleteElement}(k)$: $k$ 番目の要素を削除する。
- $\mathrm{getSum}()$: 昇順 $k$ 個の和を返す。
- $\mathrm{incrementSize}()$: $k$ を $1$ 増やす。
- $\mathrm{decrementSize}()$: $k$ を $1$ 減らす。
計算量
$O(\log n)$
但しsetを $4$ 個持っていて定数倍が重いので注意。
実装例
長方形の和集合
説明
長方形の和集合を効率よく求めるデータ構造。長方形の右上の点の追加を対数時間でサポートする。第一象限のみなので象限を増やす場合は適切に処理する必要がある。
使い方
- $\mathrm{addPoint}(x, y)$: 右上の点 $(x, y)$ の長方形を追加する。
- $\mathrm{getSum}()$: 現在の長方形群の和集合の面積を求める。
計算量
$O(\log n)$
実装例
グリッド上の幅優先探索(Grid-BFS)
説明
二次元格子上の幅優先探索。
計算量
$O(WH)$
実装例
int W, H;
char mas[500][500];
int min_cost[500][500];
int bfs(int sx, int sy, char c)
{
const int vx[] = {0, 1, 0, -1}, vy[] = {1, 0, -1, 0};
memset(min_cost, -1, sizeof(min_cost));
queue< pair< int, int > > que;
que.emplace(sx, sy);
min_cost[sx][sy] = 0;
while(!que.empty()) {
auto p = que.front(); que.pop();
if(mas[p.second][p.first] == c) return(min_cost[p.first][p.second]);
for(int i = 0; i < 4; i++) {
int nx = p.first + vx[i], ny = p.second + vy[i];
if(nx < 0 || ny < 0 || nx >= W || ny >= H) continue;
if(min_cost[nx][ny] != -1) continue;
if(mas[ny][nx] == '#') continue;
min_cost[nx][ny] = min_cost[p.first][p.second] + 1;
que.emplace(nx, ny);
}
}
return(-1);
}問題例
単一始点最短路(Dijkstra)
説明
負辺のない単一始点全点間最短路を求めるアルゴリズム。負辺が無いと仮定すると、各地点でもっとも近いところから距離が確定していく。距離順でソートされたヒープを用いると、効率よく距離を確定していくことができる。
使い方
- Dijkstra(g, s, t): 重み付き有向グラフ $g$ 上で, 頂点 $s$ から $t$ への最短路を求める。ただし非連結の時 $-1$ を返す。
計算量
$O(E \log V)$
$V$: 頂点数, $E$: 辺数
実装例
問題例
- 検証済AOJ GPL_1_A 単一始点最短経路
- AOJ0212 高速バス
- AOJ1156 ちょろちょろロボット
- AOJ2151 Brave Princess Revisited
- AOJ0596 タクシー
- AOJ1138 Traveling by Stagecoach
- AOJ1150 崖登り
- AOJ2021 お姫様の危機
- AOJ0155 スパイダー人 (経路復元)
- AOJ0562 JOI 国の買い物事情
- AOJ1162 離散的速度
- AOJ2672 郵便局員を救え
- AOJ0601 フクロモモンガ
- AOJ0605 現代的な屋敷
- AOJ1183 鎖中経路
- AOJ2585 一日乗車券
参考資料
全点対間最短路(Warshall-Floyd)
説明
隣接行列で表されるグラフの全点間最短路を求めるアルゴリズム。負辺路が存在する場合はそれも検出する(ある頂点 $k$ から $k$ への最短路が負ならば負閉路が存在)。
使い方
- Warshall(g): 隣接行列 $g$ 上の全点対間最短路を求める
隣接行列 $g$ の各要素は最初に $INF$ で初期化しておく必要がある。ただし $INF \ge 2^{30}$ のときオーバーフローするので注意。
計算量
$O(V^3)$
$V$: 頂点数
実装例
応用 1: 辺の追加
現在のグラフに辺を追加する場合に限り, 更新を$O(N^3)$ ではなく $O(N^2)$ で行える. 追加した辺に影響する範囲のみを更新するようにする.
問題例
- 検証済AOJ GPL_1_C 全点対間最短経路
- AOJ0117 大工の褒美
- AOJ0200 青春の片道切符
- AOJ0189 便利な町
- AOJ2005 Water Pipe Construction
- AOJ2200 Mr. Rito Post Office
- AOJ1182 鉄道乗り継ぎ
- AOJ0526 船旅 (応用1)
参考資料
最小全域木(Prim)
説明
最小全域木(全域木のうち、その辺群の重みの総和が最小になる木)を求めるアルゴリズム。既に到達した頂点集合からまだ到達していない頂点集合への辺のうち、コストが最小のものを選んでいくことによって、最小全域木を構成している。
計算量
$O(E \log V)$
$V$: 頂点数, $E$: 辺数
実装例
問題例
最小全域木(Kruskal)
説明
最小全域木(全域木のうち、その辺群の重みの総和が最小になる木)を求めるアルゴリズム。Union-Findを用いて辺集合にある辺を加えて閉路を作らないか判定しながら、辺を重みが小さい順に走査する。
使い方
Union-Find が必要
計算量
$O(E \log V)$
$V$: 頂点数, $E$: 辺数
実装例
問題例
最小全域有向木(Chu-Liu/Edmond)
説明
頂点 $r$ を根とする最小全域有向木を求めるアルゴリズム。頂点 $r$ から全ての頂点への経路が存在する木のうち最小コストのものを求める。
基本的には各頂点に入る辺のうち最小コストの辺を選ぶ。これらの辺からなるグラフが木ならそれが解。それ以外なら有向閉路が含まれているので閉路を縮約して適切に処理して, 閉路がなくなるまで再帰的に呼び出すことを繰り返す。
使い方
強連結成分分解 が必要
計算量
$O(VE)$
$V$: 頂点数, $E$: 辺数
実装例
問題例
最小費用流(Primal-Dual)
説明
最小費用流を最短路反復で解くアルゴリズム。始点から終点までの重みの最短路を求め、そこに流せる限り流す。これを流したい分だけ流しきるまで繰り返す。最短路の計算は、ポテンシャル $h$ を用いて負辺がないように変換して Dijkstra法 で求める。
計算量
$O(FE \log V)$
実装例
問題例
最大流(Dinic)
説明
最大流を求める。最短の増加パスを探して、そこにフローを流していくことを繰り返す。そのような経路がなくなったら残余パスでもう一度それを繰り返す。それでも、流せなくなったら終了する。実際の計算量よりも高速に動作することが知られている。
計算量
$O(E V^2)$
実装例
問題例
二部グラフの最大マッチング(Bipartite-Matching)
説明
グラフ $G=(V, E)$ において, $V$ が $2$ つの部分集合 $X$ と $Y$ に分割され, $E$ のどの辺も一方の端点は $X$ に, もう一方の端点は $Y$ に属しているとき, $G$ を 二部グラフ という.
グラフ $G=(V, E)$ において, $M$ が $E$ の部分集合でかつ $M$ のどの $2$ 辺も共通の端点をもたないとき, $M$ を $G$ の マッチング といい, 辺の本数が最大であるマッチングを 最大マッチング という.
ここでは, 二部グラフの最大マッチングを最大流のアルゴリズムを利用して求める。
計算量
$O(VE)$
実装例
何かと便利なので, 生存しているとき true を入れる alive 配列を追加してある.
応用 1: 最小頂点被覆 = 最大マッチング
グラフ $G = (V, E)$ において, 各辺 $e$ について端点のいずれか少なくとも一方が $V'$ に含まれるような $V$ の部分集合 $V'$ のうち, $V'$ の頂点数が最小であるものを 最小頂点被覆 という.
Königの定理(最大マッチング最小被覆定理) では, 二部グラフについて最大マッチングの本数と最小被覆の頂点数は等しいことを示している.
応用 2: DAGの最小パス被覆 = V - 最大マッチング
グラフ $G = (V, E)$ において, そのグラフの全ての頂点が $1$ つ以上のパスに含まれるようなパスの集合をを パス被覆 という.
特に, パス被覆の中でパスの数が最小のものを 最小パス被覆 という.
DAGの最小パス被覆は二部グラフの最大マッチング問題に帰着でき, 容易に解くことができる. 具体的には頂点を倍長して, 始点を左側に, 終点を右側に配置したグラフを考える. まず $V$ 本のパスがあれば被覆できることは自明. このグラフのマッチング一組に対して必要なパスを $1$ つ減らすことができるため, $V - $ (二部グラフの最大マッチング) が最小パス被覆となる.
参考: DAGのパス被覆の問題 - antaの競技プログラミング練習日記
応用 3: 辞書順最小
ある最大マッチングの状態から, 貪欲に上の頂点から順にフローを押し戻してより番号が小さいものが使えないか試していくことで辞書順最小の最大マッチングを求めることができる. (事前に辺について辞書順にソートしておく必要がある.)
応用 4: 押し戻す, 加える
二部グラフが変化するときについて, 変化が微妙なときは現在のマッチングの状態をもとに, それを押し戻したり新たに加えたりして少ない計算量で修正することが出来る.
以下では頂点追加と削除を実装している.
問題例
- 検証済AOJ GRL_7_A 2部マッチング
- AOJ2251 Merry Christmas (応用 2)
- AOJ0334 Amidakuji (応用 3)
Low-Link
説明
橋や関節点を効率よく求める際に有効なアルゴリズム。
グラフをDFSして, $\mathrm{ord}[idx] := $ DFS で頂点に訪れた順番, $\mathrm{low}[idx] := $ 頂点 $idx$ からDFS木の葉方向の辺を $0$ 回以上, 後対辺を $1$ 回以下通って行ける頂点の $ord$ の最小値 を各頂点について求める。
使い方
Union-Find が必要
計算量
$O(E + V)$
$V$: 頂点数, $E$: 辺数
実装例
関節点(Articulation-Points)
説明
low-link の結果を用いて関節点を効率よく求める。
DFS木の木の根については, 子が $2$ つ以上なら関節点, それ以外の頂点 $v$ については, $\mathrm{ord}[u] \le \mathrm{low}[v]$ となる $v$ の子 $u$ が存在するとき関節点となる。
使い方
Low-Link が必要
計算量
$O(V + E)$
$V$: 頂点数, $E$: 辺数
実装例
問題例
強連結成分分解(Strongly-Connected-Components)
説明
強連結成分分解する。
計算量
$O(V + E)$
実装例
struct StronglyConnectedComponents
{
vector< vector< int > > gg, rg;
vector< pair< int, int > > edges;
vector< int > comp, order, used;
StronglyConnectedComponents(size_t v) : gg(v), rg(v), comp(v, -1), used(v, 0) {}
void add_edge(int x, int y)
{
gg[x].push_back(y);
rg[y].push_back(x);
edges.emplace_back(x, y);
}
int operator[](int k)
{
return (comp[k]);
}
void dfs(int idx)
{
if(used[idx]) return;
used[idx] = true;
for(int to : gg[idx]) dfs(to);
order.push_back(idx);
}
void rdfs(int idx, int cnt)
{
if(comp[idx] != -1) return;
comp[idx] = cnt;
for(int to : rg[idx]) rdfs(to, cnt);
}
void build(vector< vector< int > > &t)
{
for(int i = 0; i < gg.size(); i++) dfs(i);
reverse(begin(order), end(order));
int ptr = 0;
for(int i : order) if(comp[i] == -1) rdfs(i, ptr), ptr++;
t.resize(ptr);
set< pair< int, int > > connect;
for(auto &e : edges) {
int x = comp[e.first], y = comp[e.second];
if(x == y) continue;
if(connect.count({x, y})) continue;
t[x].push_back(y);
connect.emplace(x, y);
}
}
};問題例
二重辺連結成分分解(Biconnected-Components)
説明
二重辺連結成分分解する。副作用として橋を返す。
辺 $(u, v)$ は $\mathrm{ord}[u] \lt \mathrm{low}[v]$ のとき橋となる。
使い方
Low-Link が必要
計算量
$O(V + E)$
実装例
問題例
HL分解(Centroid-Path-Decomposition)
説明
木をHL分解する。結構癖のある書き方みたい。
計算量
$O(V + E)$
実装例
問題例
木の直径
説明
非負の重み付き無向木の直径を求める。適当な頂点 $s$ から最も遠い頂点 $u$ を求める。次に $u$ から最も遠い頂点 $v$ を求める。このとき、($u$, $v$) が最遠頂点対であり、すなわち木の直径である。
計算量
$O(E)$
実装例
問題例
素因数分解
説明
素因数分解する。
計算量
$O(\sqrt N)$
実装例
応用: 約数の個数
ある自然数 $n$ を素因数分解して $n = \prod_{i=1}^r {p_i}^{a_i}$ ($p_i$ は素数) の形で表せたとする。
自然数 $n$ の約数の個数 $d(n)$ は $d(n) = \prod_{i=1}^r (a_i + 1)$ と等しいことが示せる。
問題例
素因数分解
説明
約数を列挙する。
計算量
$O(\sqrt N)$
実装例
応用: 高度合成数
高度合成数とは, 自然数でそれ未満のどの自然数よりも約数の個数が多いものをいう。
高度合成数の表より, $10^9$ 以下の高度合成数の最大値は $735134400$ の $1344$ 個である。
問題例
繰り返し二乗法
説明
冪乗を高速に求めるアルゴリズム。すべての自然数は $2$ の冪乗和の組み合わせで表すことができるという性質を利用している。 $N$ を $2$ の冪乗和で表すと $N = 2^{K_1} + 2^{K_2} + 2^{K_3} + \dots$ となる。よって $x^N = x^{2^{K_1}} \times x^{2^{K_2}} \times x^{2^{K^3}} \times \dots$。$2$ 進数で操作すればよいので, $1$ のビットが立つ部分 $i$ について, 解に $x^i$ を掛けていく。
計算量
$O(\log N)$
実装例
問題例
素数列挙(Sieve of Eratosthenes)
説明
エラトステネスの篩による素数列挙アルゴリズム。指定された自然数以下の全ての素数を発見するための単純なアルゴリズム。具体的には, まず $2$ の倍数を除外する。次に $3$ の倍数を除外する。 $4$ は除外されているので $5$ の倍数を除外する。 $6$ は除外されているので $7$ を除外する。... というふうに, 素数の倍数を貪欲に除外していく。
計算量
$O(N \log \log N)$
実装例
問題例
平面幾何の基本要素
点(Point)
点同士の加減乗算, スカラー倍などは operator で定義している。
その他のメンバ関数の意味は以下の通り。
- $\mathrm{norm}() := x^2 + y^2$ (大きさの $2$ 乗)
- $\mathrm{abs}() := \sqrt {x^2 + y^2}$ (大きさ)
- $\mathrm{arg}() := \tan^{-1} \frac y x$ (逆正接, $[-\pi, \pi]$ の範囲で返す)
- $\mathrm{rotate}(\theta) := (x\cos\theta-y\sin\theta, x\sin\theta+y\cos\theta)$ (反時計周りに $\theta$ 回転)
- $\mathrm{rotate90}() := (x\cos \frac \pi 2 -y\sin \frac \pi 2,x \sin \frac \pi 2 +y \cos \frac \pi 2) = (-y, x)$ (反時計周りに $\frac \pi 2$ 回転)
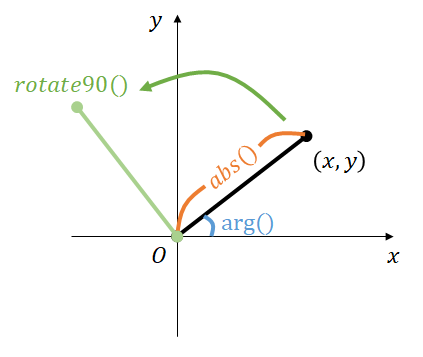
また, 点同士の演算に以下の関数も定義している。$a = (x_1, y_1), b = (x_2, y_2)$ とする。
- $\mathrm{cross}(a, b) := a \times b = x_1 y_2 + x_2 y_1 = |a||b|\sin\theta$ (外積)
- $\mathrm{dot}(a, b) := a \cdot b = x_1 x_2 + y_1 y_2 = |a||b|\cos\theta$ (内積)
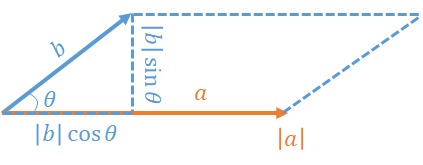
- $\mathrm{RadianToDegree}(r) := r [rad] \to d [°]$
- $\mathrm{DegreeToRadian}(d) := d [°] \to r[rad]$
- $\mathrm{GetAngle(a, b, c)} := 3$ 点 $a \to b \to c$ の角度 $[0, \pi]$
直線(Line)
直線は, それが通る $2$ 点 $a, b$ を用いて表現している。
線分(Segment)
線分は, 端点 $a, b$ を用いて表現している。
円(Circle)
円は, 中心の座標 $p$ と半径 $r$ で表現している。
その他
- 多角形(Polygon)
- 線分集合(Segments)
- 直線集合(Lines)
- 円集合(Circles)
- $2$ 点(PointPoint)
実装例
点の進行方向
説明
与えられた $3$ 点の位置関係は以下の $5$ つに分類できる。
- $a \to b$ 反時計回りの方向に $c$
- $a \to b$ 時計回りの方向に $c$
- $c \to a \to b$ の順に並ぶ
- $a \to b \to c$ の順に並ぶ
- $a \to c \to b$ の順に並ぶ
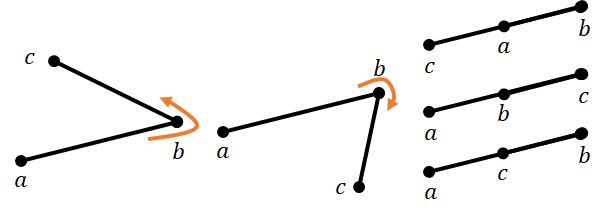
判定アルゴリズムは以下の通り。$a$ から $b$ へ向かうベクトルを $\vec b$, $a$ から $c$ へ向かうベクトルを $\vec c$ とする。
- $\vec b \times \vec c \gt 0$ のとき, $\vec c$ は $\vec b$ から反時計回りの位置にあると判定できる。(外積は右ねじの方向を向く)
- $\vec b \times \vec c \lt 0$ のとき, $\vec c$ は $\vec b $ から時計回りの位置にあると判定できる。
- $\vec b \times \vec c = 0$ のとき $3$ 点が直線状に並ぶ。$\vec b \cdot \vec c \lt 0$ のとき, $c \to a \to b$ の順に並ぶと判定できる。($\cos \theta$ は $|\theta| \gt \frac \pi 2$ のとき負)
- $|\vec b| \lt |\vec c|$ のとき, $a \to b \to c$ の順に並ぶと判定できる。
- それ以外のとき, $a \to c \to b$ の順に並ぶと判定できる。
実装例
int ccw(const Point &a, Point b, Point c)
{
b = b - a, c = c - a;
if(cross(b, c) > EPS) return +1;
if(cross(b, c) < -EPS) return -1;
if(dot(b, c) < 0) return +2;
if(b.norm() < c.norm()) return -2;
return 0;
}直線の直交・平行判定
直交判定
$\mathrm{Parallel}(a, b):=$ 直線 $a, b$ が平行ならば true
内積 $a \cdot b = |a||b|\cos\theta$ をよく見ると $\theta = \pm \frac \pi 2$ のとき $\cos\theta = 0$ となる。
平行判定
$\mathrm{Orthogonal}(a, b):=$ 直線 $a, b$ が直交していれば true
外積 $a \times b = |a||b|\sin\theta$ をよく見ると $\theta = 0, \pi$ のとき $\sin\theta = 0$ となる。
実装例
bool Parallel(const Line& a,const Line& b){
return abs(cross(a.b - a.a, b.b - b.a)) < EPS;
}
bool Orthogonal(const Line& a,const Line& b){
return abs(dot(a.a - a.b, b.a - b.b)) < EPS;
}射影・反射
射影
$\mathrm{Projection}(l, p):=$ 点 $p$ の直線 $l$ に対する射影を求める
点 $p$ から直線 $l = \vec {ab}$ に垂線をおろしたときの交点 $x$ を点 $p$ の射影と呼ぶ。
反射
$\mathrm{Reflection}(l, p):=$ 点 $p$ の直線 $l$ に対する反射を求める
直線 $l = \vec {ab}$ を対称軸として点 $p$ と線対称の位置にある点 $x$ を $p$ の反射と呼ぶ。
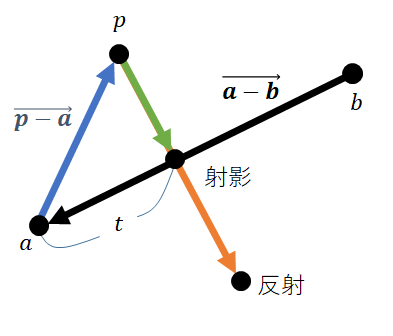
実装例
Point Projection(const Line& l, const Point& p){
double t = dot(p - l.a, l.a - l.b) / (l.a - l.b).norm();
return l.a + (l.a - l.b) * t;
}
Point Projection(const Segment& l, const Point& p){
double t = dot(p - l.a, l.a - l.b) / (l.a - l.b).norm();
return l.a + (l.a - l.b) * t;
}
Point Reflection(const Line& l, const Point& p){
return p + (Projection(l, p) - p) * 2.0;
}距離
点(Point)と点(Point)の距離
点 $a$ と点 $b$ の距離は $|\overrightarrow {a- b}|$ である。
直線(Line)と点(Point)の距離
直線 $l$ と点 $p$ の距離は, 点 $p$ と点 $p$ の直線 $l$ に対する射影との距離である。
直線(Line)と直線(Line)の距離
直線 $l$ と直線 $m$ の距離は, $l, m$ が交差しているとき $0$, 交差していない時は直線 $l$ 上の適当な点 $l.a$ と点 $l.a$ の直線 $m$ に対する射影との距離である。
線分(Segment)と点(Point)の距離
点 $p$ の線分 $l$ に対する射影 $r$ を求める。
点 $r$ が線分 $l$ 上にあればそれと点 $p$ との距離, なければ線分 $l$ の両端の点 $l.a, l.b$ と点 $r$ との距離の min となる。
線分(Segment)と線分(Segment)の距離
線分 $a$ と線分 $b$ との距離を求める。
$a$ と $b$ が交差している場合は $0$, 交差していない場合は線分と点との距離に帰着させる。$a, b$ の両端の点と線分との距離の min をとればよい。
直線(Line)と線分(Segment)の距離
直線 $l$ と線分 $s$ の距離は, 交差している場合は $0$, 交差していない場合は $l$ と線分 $s$ の端点 $s.a, s.b$ との距離の min となる。
実装例
double Distance(const Point& a,const Point& b){
return (a - b).abs();
}
double Distance(const Line& l,const Point& p) {
return (p - Projection(l, p)).abs();
}
double Distance(const Line& l,const Line& m) {
return Intersect(l, m) ? 0 : Distance(l, m.a);
}
double Distance(const Segment& s,const Point& p){
Point r = Projection(s, p);
if (Intersect(s, r)) return (r - p).abs();
return min((s.a - p).abs(), (s.b - p).abs());
}
double Distance(const Segment& a,const Segment& b){
if(Intersect(a, b)) return 0;
return min(min(Distance(a, b.a), Distance(a, b.b)), min(Distance(b, a.a), Distance(b, a.b)));
}
double Distance(const Line& l,const Segment& s) {
if (Intersect(l, s)) return 0;
return min(Distance(l, s.a), Distance(l, s.b));
}交差判定
実装例
交点
実装例
凸多角形判定
説明
与えられた多角形が凸多角形かどうか判定する。点を順番に見ていき隣接 $3$ 点について点の進行方向が逆向きのものがないか確かめれば良い。
計算量
$O(N)$
実装例
bool IsConvex(const Polygon& p){
int n = p.size();
for(int i = 0; i < n; i++){
if(ccw(p[(i + n - 1) % n], p[i], p[(i + 1) % n]) == -1) return false;
}
return true;
}凸包
説明
凸包を Andrew's Monotone Chain によって求める。
アルゴリズムの概要は以下の通り。
- 点を x 座標の昇順でソートする。 x が同じ場合は y 座標の昇順で比較する。
- 上側凸包を求める。
- 凸包の点をスタックで管理することとし, x 座標の昇順にスタックに点を $1$ つずつ追加していく。点を含めると凸でなくなる場合(点の進行方向 ccw を用いて判定) は凸になるまでスタックから点を取り除く。
- 下側凸包を求める。
計算量
$O(N \log N)$
実装例
Polygon Convex_Hull(Polygon& p){
int n = p.size(), k = 0;
if(n >= 3){
sort(p.begin(), p.end());
vector< Point > ch(2 * n);
for(int i = 0; i < n; ch[k++] = p[i++]){
while(k >= 2 && cross(ch[k - 1] - ch[k - 2], p[i] - ch[k - 1]) < 0) --k;
}
for(int i = n - 2, t = k + 1; i >= 0; ch[k++] = p[i--]){
while(k >= t && cross(ch[k - 1] - ch[k - 2], p[i] - ch[k - 1]) < 0) --k;
}
ch.resize(k - 1);
return ch;
} else {
return p;
}
}点 - 多角形包含判定
実装例
線分アレンジメント
平行な線分が重なるときは MergeSemgnets を呼び出してから処理する.
実装例
凸多角形の切断
説明
凸多角形を直線 $l$ で切断し, その左側を返す。
直線より左側にあるものと, 直線 $l$ との交点を残している。
実装例
多角形の面積
実際の面積の 2 倍が返されるので注意
実装例
凸多角形の直径
説明
凸多角形の直径を求める。ここで凸多角形の直径とは最も遠い頂点間の距離である。
最遠点対は凸包上の $2$ 点のいずれかなので, ある点集合が与えられたとするとその凸包をとって直径を求めることで最遠点対を求めることができる。
計算量
$O(N)$
実装例
double Convex_Diameter(Polygon& p){
int n = p.size();
int is = 0, js = 0;
for(int i = 1; i < n; i++){
if(p[i].y > p[is].y) is = i;
if(p[i].y < p[js].y) js = i;
}
double maxdis = (p[is] - p[js]).norm();
int maxi, maxj, i, j;
i = maxi = is;
j = maxj = js;
do {
if(cross(p[(i + 1) % n] - p[i], p[(j + 1) % n] - p[j]) >= 0){
j = (j + 1) % n;
} else {
i = (i + 1) % n;
}
if((p[i] - p[j]).norm() > maxdis){
maxdis = (p[i] - p[j]).norm();
maxi = i; maxj = j;
}
} while (i != is || j != js);
return maxdis;
}接尾辞配列(Suffix-Array)
説明
接尾辞配列。蟻本には $O(N \log^2 N)$ の実装が載っているが, ここでは $O(N \log N)$ の実装を扱う。SA-IS を使えば線形時間で構築できる。
計算量
- Build_SA: $O(N \log N)$
- lower_bound, lower_upper_bound: $O(M\log N)$
- Build_LCA: $O(N)$
実装例
問題例
ローリングハッシュ(Rolling-Hash)
説明
文字列の一致判定やLCPをハッシュを使って高速に求めるもの。
計算量
- RollingHash: $O(N)$
- get, connect: $O(1)$
- LCP: $O(\log N)$
実装例
問題例
Z-algorithm
説明
ある文字列 $S$ が与えられているとする。Z-algorithm では, それぞれの $i$ について $S$ と $S[i,|S|]$ の最長共通接頭辞の長さを記録した配列を線形時間で構築するアルゴリズムである。
具体例を以下に示す。例えば $i = 5$ "aaaab" のときの最長共通接頭辞は "aaa", つまり $3$ 文字である。
aaabaaaab
921034210計算量
$O(|S|)$
実装例
問題例
参考資料
Manacher
説明
ある文字列 $S$ が与えられているとする。Manacher では, それぞれの $i$ について文字 $i$ を中心とする最長回文の半径を記録した配列を線形時間で構築するアルゴリズムである。
具体例を以下に示す。例えば $i = 6$ を中心とする最長回文は "aba" つまり $2$ である。
abaaababa
121412321計算量
$O(|S|)$
実装例
Manacharよりも Manachan の方が可愛いので Manachan にしてあります(?)
問題例
参考資料
Aho-Corasick
説明
パターンマッチングを行う。
計算量
$O(N + M)$
$N$: 入力文字列の長さ
$M$: パターンの文字列の長さの合計
実装例
パターンごとのマッチングの個数が不要な場合はset_union() を消したほうがよさそうです(重そうなので)。
参考資料
一次元累積和
説明
$1$ 次元の累積和。前計算として事前に累積させておけば, 累積和を $O(1)$ で求めることが出来る。
使い方
- set(k, x): 要素 $k$ に値 $x$ を加える
- build(): 累積和を構築する
- query(k): 区間 $[0, k]$ の和を求める
計算量
- build: $O(n)$
- add, query: $O(1)$
実装例
問題例
二次元累積和
説明
点add, 矩形sumの $2$ 次元の累積和。前計算として事前に累積させておけば, 累積和を $O(1)$ で求めることが出来る。
使い方
- set(x, y, z): 要素 $(x, y)$ に値 $z$ を加える
- build(): 累積和を構築する
- query(sx, sy, gx, gy): 左上 $[sx, sy]$, 右下 $(gx, gy)$ の矩形内の和を求める(半開区間)
計算量
- build: $O(WH)$
- add, query: $O(1)$
実装例
問題例
参考資料
サイコロ
サイコロを転がします。
$l:=$ 左, $r:=$ 右, $f:=$ 前, $b:=$ 後ろ, $d:=$ 下, $u:=$ 上
実装例
分解可能問題
説明
クエリ問題が分解可能であるとは
- 要素 $1$ つだけのデータ $[e]$ に対するクエリを $q([e])$ と表すとき, 要素列に対するクエリは $q([e_1, e_2, \dotsc, e_n]) = q([e_1]) \star q([e_2]) \star \dotsb \star q([e_n])$ となる演算子 $\star$ (結合法則を満たす) によって表すことができる
ものをいう。ここでは分解可能問題に対する静的なデータ構造を与えられた時にインクリメンタルなデータ構造にしている。
計算量
$n$ 要素の静的データ構造が $T(n)$ で構築できるとき, $n$ 回の追加にかかる計算量 $O(T(n)\log n)$
$n$ 要素の静的データ構造に対するクエリと $\star$ が $U(n)$ で応答できるとき, $n$ 回のクエリにかかる計算量 $O(U(n)\log n)$
実装例
静的なデータ構造 $T_1$ と $T_2$ を結合する $T_1 + T_2$ オペレータを定義する必要がある。また, クエリに応答する際には, 添字演算子[] を使いデータ構造を取り出す。
問題例
- 検証済ECR 16 F. String Set Queries (Submittion: #24912583)