平面幾何の基本要素
点(Point)
点同士の加減乗算, スカラー倍などは operator で定義している。
その他のメンバ関数の意味は以下の通り。
- $\mathrm{norm}() := x^2 + y^2$ (大きさの $2$ 乗)
- $\mathrm{abs}() := \sqrt {x^2 + y^2}$ (大きさ)
- $\mathrm{arg}() := \tan^{-1} \frac y x$ (逆正接, $[-\pi, \pi]$ の範囲で返す)
- $\mathrm{rotate}(\theta) := (x\cos\theta-y\sin\theta, x\sin\theta+y\cos\theta)$ (反時計周りに $\theta$ 回転)
- $\mathrm{rotate90}() := (x\cos \frac \pi 2 -y\sin \frac \pi 2,x \sin \frac \pi 2 +y \cos \frac \pi 2) = (-y, x)$ (反時計周りに $\frac \pi 2$ 回転)
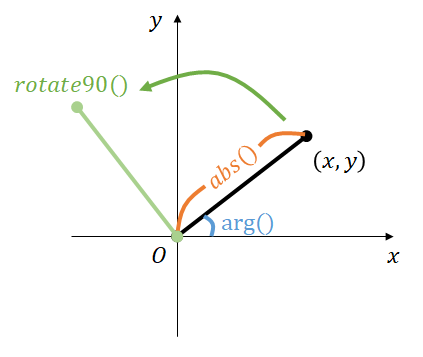
また, 点同士の演算に以下の関数も定義している。$a = (x_1, y_1), b = (x_2, y_2)$ とする。
- $\mathrm{cross}(a, b) := a \times b = x_1 y_2 + x_2 y_1 = |a||b|\sin\theta$ (外積)
- $\mathrm{dot}(a, b) := a \cdot b = x_1 x_2 + y_1 y_2 = |a||b|\cos\theta$ (内積)
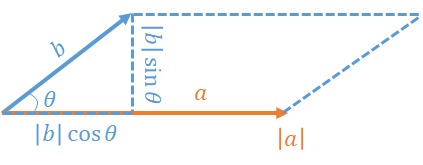
- $\mathrm{RadianToDegree}(r) := r [rad] \to d [°]$
- $\mathrm{DegreeToRadian}(d) := d [°] \to r[rad]$
- $\mathrm{GetAngle(a, b, c)} := 3$ 点 $a \to b \to c$ の角度 $[0, \pi]$
直線(Line)
直線は, それが通る $2$ 点 $a, b$ を用いて表現している。
線分(Segment)
線分は, 端点 $a, b$ を用いて表現している。
円(Circle)
円は, 中心の座標 $p$ と半径 $r$ で表現している。
その他
- 多角形(Polygon)
- 線分集合(Segments)
- 直線集合(Lines)
- 円集合(Circles)
- $2$ 点(PointPoint)
実装例